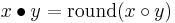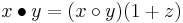Machine epsilon
Machine epsilon gives an upper bound on the relative error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science. The quantity is also called macheps or unit roundoff, and it has the symbols Greek epsilon  or bold Roman u.
or bold Roman u.
Contents |
Values for standard hardware floating point arithmetics
The following values of machine epsilon are encountered in practice.
| IEEE 754 - 2008 | Common name | C++ data type | Base  |
Fractional digits  |
Machine epsilon 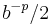 |
C++ or Python formula | Value |
|---|---|---|---|---|---|---|---|
| binary16 | half precision | not available | 2 | 10 | 2 -11 | pow (2, -11) | 4.88e-04 |
| binary32 | single precision | float | 2 | 23 | 2 -24 | pow (2, -24) | 5.96e-08 |
| binary64 | double precision | double | 2 | 52 | 2 -53 | pow (2, -53) | 1.11e-16 |
| binary128 | quad(ruple) precision | long double | 2 | 112 | 2 -113 | pow (2, -113) | 9.63e-35 |
Machine epsilon depends on both the kind of floating point numbers and the kind of rounding. There are several possible rounding modes for use in floating point arithmetic. The four most commonly used rounding modes are relevant because most general-purpose computer chips conform to the 1985 IEEE standard and the 2008 revision. Other schemes are of interest, but while the standard allows several methods of rounding, programming languages and systems vendors do not provide methods to change the rounding mode from the default: round-to-nearest with the tie-breaking scheme round-to-even.
Formal definition
Rounding is a procedure for choosing the representation of a real number in a floating point number system. For a number system and a rounding procedure, machine epsilon is the maximum relative error of the chosen rounding procedure.
Some background is needed to determine a value from this definition. A floating point number system is characterized by a radix which is also called the base,  , and by the number of significant figures,
, and by the number of significant figures,  . (The whole number out in front is yet another digit.) All the numbers with the same exponent,
. (The whole number out in front is yet another digit.) All the numbers with the same exponent,  , have the spacing,
, have the spacing, 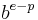 . The spacing changes at the numbers that are perfect powers of
. The spacing changes at the numbers that are perfect powers of  ; the spacing on the side of larger magnitude is
; the spacing on the side of larger magnitude is  times larger than the spacing on the side of smaller magnitude.
times larger than the spacing on the side of smaller magnitude.
Since machine epsilon is a bound for relative error, it suffices to consider numbers with exponent 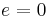 . It also suffices to consider positive numbers. For the usual round-to-nearest kind of rounding, the absolute rounding error is at most half the spacing, or
. It also suffices to consider positive numbers. For the usual round-to-nearest kind of rounding, the absolute rounding error is at most half the spacing, or 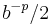 . This value is the biggest possible numerator for the relative error. The denominator in the relative error is the number being rounded, which should be as small as possible to make the relative error large. The worst relative error therefore happens when rounding is applied to numbers of the form
. This value is the biggest possible numerator for the relative error. The denominator in the relative error is the number being rounded, which should be as small as possible to make the relative error large. The worst relative error therefore happens when rounding is applied to numbers of the form 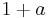 where
where  is between
is between 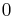 and
and 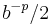 . All these numbers round to
. All these numbers round to 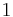 with relative error
with relative error 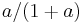 . The maximum occurs when
. The maximum occurs when  is at the upper end of its range. The
is at the upper end of its range. The 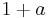 in the denominator hardly matters, so it is left off for expediency, and just
in the denominator hardly matters, so it is left off for expediency, and just 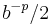 is taken as machine epsilon. As has been shown here, the relative error is worst for numbers that round to
is taken as machine epsilon. As has been shown here, the relative error is worst for numbers that round to 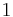 , so machine epsilon also is called unit roundoff meaning roughly "the maximum error that can occur when rounding to the unit value".
, so machine epsilon also is called unit roundoff meaning roughly "the maximum error that can occur when rounding to the unit value".
Arithmetic model
Numerical analysis uses machine epsilon to study the effects of rounding error. The actual errors of machine arithmetic are far too complicated to be studied directly, so instead, the following simple model is used. The IEEE arithmetic standard says all floating point operations are done as if it were possible to perform the infinite-precision operation, and then, the result is rounded to a floating point number. Suppose (1)  ,
,  are floating point numbers, (2)
are floating point numbers, (2) 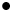 is an arithmetic operation on floating point numbers such as addition or multiplication, and (3)
is an arithmetic operation on floating point numbers such as addition or multiplication, and (3) 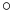 is the infinite precision operation. According to the standard, the computer calculates:
is the infinite precision operation. According to the standard, the computer calculates:
By the meaning of machine epsilon, the relative error of the rounding is at most machine epsilon in magnitude, so:
where  in absolute magnitude is at most
in absolute magnitude is at most  or u. The books by Demmel and Higham in the references can be consulted to see how this model is used to analyze the errors of, say, Gaussian elimination.
or u. The books by Demmel and Higham in the references can be consulted to see how this model is used to analyze the errors of, say, Gaussian elimination.
Variant definitions
The IEEE standard does not define the terms machine epsilon and unit roundoff, so people are free to use different meanings which can cause some confusion.
The definition given here for machine epsilon is the one used by LAPACK and by James Demmel, a student and colleague of the primary architect for the IEEE standard, Prof. William Kahan. Most numerical analysts use the words machine epsilon and unit roundoff interchangeably and with this meaning.
Sometimes machine epsilon means the spacing of floating point numbers with zero exponent. By this definition,  equals the value of the unit in the last place relative to 1, and then for the round-to-nearest kind of rounding procedure, u
equals the value of the unit in the last place relative to 1, and then for the round-to-nearest kind of rounding procedure, u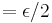 . Prof. Nicholas Higham uses this scheme of definitions. The MATLAB eps function returns this
. Prof. Nicholas Higham uses this scheme of definitions. The MATLAB eps function returns this  , not the unit roundoff.
, not the unit roundoff.
How to determine machine epsilon
Where standard libraries do not provide precomputed values (as float.h does with FLT_EPSILON, DBL_EPSILON and LDBL_EPSILON for C and C++), the best way to determine machine epsilon is to refer to the table, above, and use the appropriate pow formula. Computing machine epsilon is often given as a textbook exercise. The following examples compute machine epsilon in the sense of the spacing of the floating point numbers at 1 rather than in the sense of the unit roundoff.
Note that results depend on the particular floating-point format used, such as float, double, long double, or similar as supported by the programming language, the compiler, and the runtime library for the actual platform.
Some formats supported by the processor might be not supported by the chosen compiler and operating system. Other formats might be emulated by the runtime library, including arbitrary-precision arithmetic available in some languages and libraries.
In a strict sense the term machine epsilon means the 1+eps accuracy directly supported by the processor (or coprocessor), not some 1+eps accuracy supported by a specific compiler for a specific operating system, unless it's known to use the best format.
A trivial example is the machine epsilon for integer arithmetic on processors without floating point formats; it is 1, because 1+1=2 is the smallest integer greater than 1.
IEEE 754 floating-point formats monotonically increase over positive values and monotonically decrease over negative values. They also have the property that where f(x) is the reinterpretation of x from an unsigned or twos-complement integer format to a floating-point format of the same width, and 0 < |f(x)| < ∞, |f(x+1) − f(x)| ≥ |f(x) − f(x−1)|. In languages that allow type punning and always use IEEE 754-1985, we can exploit this to compute a machine epsilon in constant time. For example, in C:
typedef union { long long i64; double d64; } dbl_64; double machine_eps (double value) { dbl_64 s; s.d64 = value; s.i64++; return s.d64 - value; }
This will give a result of the same sign as value. If a positive result is always desired, the return statement of machine_eps can be replaced with:
return (s.i64 < 0 ? value - s.d64 : s.d64 - value);
64-bit doubles give 2.220446e-16, which is 2-52 as expected.
Approximation using C
The following C program does not actually determine the machine epsilon; rather, it determines a number within a factor of two (one order of magnitude) of the true machine epsilon, using a linear search.
#include <stdio.h> int main( int argc, char **argv ) { float machEps = 1.0f; printf( "current Epsilon, 1 + current Epsilon\n" ); do { printf( "%G\t%.20f\n", machEps, (1.0f + machEps) ); machEps /= 2.0f; // If next epsilon yields 1, then break, because current // epsilon is the machine epsilon. } while ((float)(1.0 + (machEps/2.0)) != 1.0); printf( "\nCalculated Machine epsilon: %G\n", machEps ); return 0; }
Abridged Output
$ cc machine_epsilon.c; ./a.out current Epsilon, 1 + current Epsilon 1 2.00000000000000000000 0.5 1.50000000000000000000 ... 0.000244141 1.00024414062500000000 0.00012207 1.00012207031250000000 6.10352E-05 1.00006103515625000000 3.05176E-05 1.00003051757812500000 1.52588E-05 1.00001525878906250000 7.62939E-06 1.00000762939453125000 3.8147E-06 1.00000381469726562500 1.90735E-06 1.00000190734863281250 9.53674E-07 1.00000095367431640625 4.76837E-07 1.00000047683715820312 2.38419E-07 1.00000023841857910156
Calculated Machine epsilon: 1.19209E-07
Approximation using Java
A similar Java method:
private void calculateMachineEpsilonFloat() {
float machEps = 1.0f;
do {
machEps /= 2.0f;
}
while ((float)(1.0 + (machEps/2.0)) != 1.0);
System.out.println( "Calculated machine epsilon: " + machEps );
}
Another Java implementation (together with a Smalltalk version) can be found in the appendix to Besset's (2000) numerical methods in Java & Smalltalk book. This appendix presents a complete implementation of MACHAR (Cody, 1988) in Smalltalk and Java.
Approximation using Haskell
main = print . last . map (subtract 1) . takeWhile (/= 1) . map (+ 1) . iterate (/2) $ 1
Approximation using Python
The following Python function uses an approximation method to determine the value of machine epsilon for an arbitrary numerical data type.
def machineEpsilon(func=float): machine_epsilon = func(1) while func(1)+func(machine_epsilon) != func(1): machine_epsilon_last = machine_epsilon machine_epsilon = func(machine_epsilon) / func(2) return machine_epsilon_last
Some examples of its output (using IPython):
In [1]: machineEpsilon(int) Out[1]: 1
In [2]: machineEpsilon(float) Out[2]: 2.2204460492503131e-16
In [3]: machineEpsilon(complex) Out[3]: (2.2204460492503131e-16+0j)
Using NumPy, the value of an inexact type's machine epsilon can be determined using the eps attribute of numpy.finfo as follows (again, in iPython):
In [1]: import numpy
In [2]: numpy.finfo(numpy.float).eps Out[2]: 2.2204460492503131e-16
In [3]: numpy.finfo(numpy.complex).eps Out[3]: 2.2204460492503131e-16
Approximation using Ada
In Ada, epsilon maybe inferred from the 'Digits attribute.[1]
Epsilon : constant Real'Base := 1.0 / (10.0 ** Real'Digits);
Approximation using Prolog
An approximation using arithmetic and recursive predicates in Prolog is:
epsilon(X):- Y is (1.0 + X), Y = 1.0, write(X). epsilon(X):- Y is X/2, epsilon(Y).
An example execution in the SWI-Prolog interpreter:
1 ?- epsilon(1.0). 1.1102230246251565e-16 true .
Notes and references
- ^ "3.5.8 Operations of Floating Point Types" "Ada Reference Manual". ISO. 2005. http://www.adaic.org/resources/add_content/standards/05rm/html/RM-3-5-8.html. Retrieved 2011-04-04.
- E. Anderson, LAPACK Users' Guide, SIAM, Philadelphia, PA, third edition, 1999.
- W. J. Cody, MACHAR: A Soubroutine to Dynamically Determine Machine Parameters, ACM Transactions on Mathematical Software, Vol. 14(4), 1988, 303-311.
- D. H. Besset, Object-Oriented Implementation of Numerical Methods, Morgan & Kaufmann, San Francisco, CA, 2000.
- J. W. Demmel, Applied Numerical Linear Algebra, SIAM, Philadelphia, PA, 1997.
- N. J. Higham, Accuracy and Stability of Numerical Algorithms, SIAM, Philadelphia, PA, second edition, 2002.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical Recipes in Fortran 77, 2nd Ed., Chap. 20.2, pp. 881-886
- G. E. Forsythe, M. A. Malcolm, C. B. Moler, "Computer Methods for Mathematical Computations", Prentice-Hall, ISBN 0-13-165332-6, 1977
See also
- Floating point, general discussion of accuracy issues in floating point arithmetic
- Ulp, unit in the last place
External links
- MACHAR, a routine (in C and Fortran) to "dynamically compute machine constants" (ACM algorithm 722)
- Diagnosing floating point calculations precision, Implementation of MACHAR in Component Pascal and Oberon based on the Fortran 77 version of MACHAR published in Numerical Recipes (Press et al., 1992).